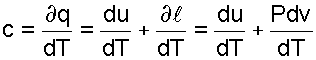
(4.21)
Воспользуемся первым законом термодинамики для получения аналитических выражений изохорной и изобарной теплоемкостей идеальных газов
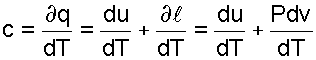 |
(4.21) |
При v=const (dv=0) из выражения (4.21) получим аналитическое выражение для изохорной теплоемкости
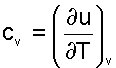 |
(4.22) |
Подставив сv в выражение дифференциала внутренней энергии при независимых переменных T и v получим выражение
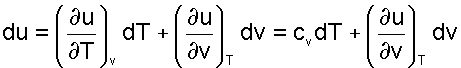 |
(4.23) |
Для идеального газа внутренняя энергия функция только одного термического параметра - температуры, т.е. (du/dv)T=0. Следовательно для идеального газа выражение (4.23) примет вид
(4.24) |
Аналитическое выражение изохорной теплоемкости идеалного газа получается из (4.24) и выражения внутренней энергии идеального газа
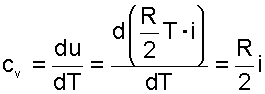 |
(4.25) |
Из выражения (4.25) следует, что изохорная теплоемкость идеального газа величина постоянная. Подставив выражение изохорной теплоемкости идеальных газов (4.25) в уравнение (4.21), получим выражение теплоемкости идеального газа в виде
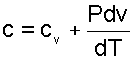 |
(4.26) |
Рассмотрим выражение (4.26) применительно к идеальному газу для изобарного процесса P=const. Второе слагаемое выражения (4.26) для идеального газа при P=const можно получить дифференцированием уравнения Менделеева-Клапейрона Pv=RT , при Р=const Pdv=RdT → Pdv/dT=R . В результате этих преобразований получаем расчетное выражение для изобарной теплоемкости идеального газа
(4.27) |
Уравнение (4.27) носит название формулы Майера. Используя формулу Майера, получим аналитическое выражение изобарной теплоемкости идеального газа
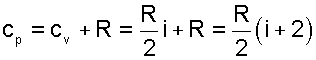 |
(4.28) |
Изобарная теплоемкость идеального газа больше изохорной теплоемкости на величину газовой постоянной.
Аналитические выражения для удельных мольных и объемных изохорных и изобарных теплоемкостей идеального газа легко получить, используя их взаимосвязь с удельными массовыми теплоемкостями (4.25) и (4.28)
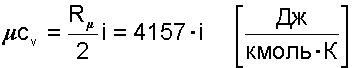 |
(4.29) |
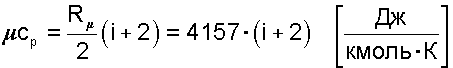 |
(4.30) |
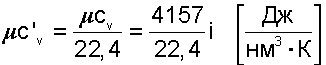 |
(4.31) |
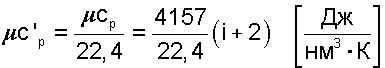 |
(4.32) |
В соответствии с молекулярно-кинетической теорией идеальных газов их изобарные и изохорные теплоемкости (выражения (4.25), (4.28)-(4.32)) величины постоянные, не зависящие от термических парметров состояния газа.
В системе единиц, основанной на калории (1ккал=4187кДж) мольная теплоемкость идеального газа определяется простым соотношением
(4.33) |
(4.34) |
| предыдущий параграф | содержание | следующий параграф |