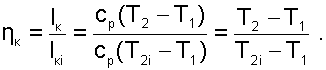
8.1.2. Влияние параметров рабочего тела на тепловую экономичность реального цикла ГТУ

Необратимость в реальном цикле ГТУ характеризуется наличием трения в адиабатных процессах сжатия 12’ и расширения 34’ рабочего тела в компрессоре и газовой турбине (рис. 8.8).

Необратимость адиабатного процесса сжатия в компрессоре характеризует адиабатный коэффициент компрессора

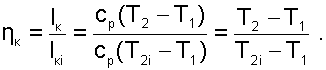(8.15)

Необратимость адиабатного процесса расширения газа в турбине характеризует внутренний относительный КПД турбины

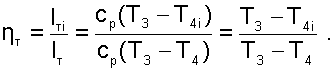(8.16)

Эти коэффициенты определяются опытным путем, для конкретной ГТУ. При расчетах ими пользуются как известными величинами или принимают их на основании справочных данных по ГТУ.

Используя эти коэффициенты, рассчитываются действительные температуры в конце адиабатных процессов

(8.17)

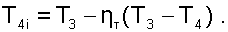(8.18)

Определение работы компрессора и турбины, подведенной и отведенной теплоты к рабочему телу и работа действительного цикла ГТУ, ведется аналогично идеальному циклу ГТУ, но с использованием реальных параметров рабочего тела

(8.19)

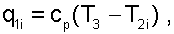(8.20)

(8.21)

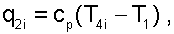(8.22)

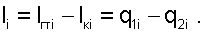(8.23)

Тепловая экономичность действительного цикла ГТУ на первом этапе характеризуется внутренним абсолютным КПД

(8.24)

Преобразовав выражение 8.24, используя соотношения 8.18, 8.20 температуру и величины ν и β

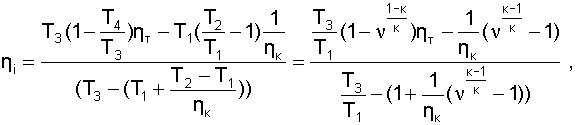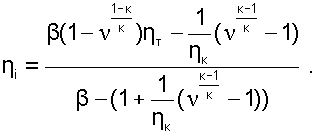(8.25)

Из уравнения 8.25 следует, что при неизменных значениях β (Т₁, Т₃) и η_Т, η_К внутренний абсолютный КПД ГТУ зависит от степени повышения давления воздуха в компрессоре ν. Графическая зависимость η_i и l_i от ν при постоянных β и η_Т, η_К, показана на рис. 8.9.

Из данных графиков видно, что имеются максимумы КПД и работы цикла, которые находятся при разных степенях повышения давления (ν_iОПТ1 и ν_iОПТ2). Оптимальное значение степени повышения давления для реальной ГТУ следует выбирать с учетом ее КПД и максимальной работы цикла, которую характеризует коэффициент работы φ. При этом получается, что ν_iОПТ2<ν_iОПТ<ν_iОПТ1, а окончательное решение этого вопроса требует технико-экономических расчетов. Так при дорогом топливе, ν_iОПТ будет иметь значение ближе к ν_iОПТ1, а при дешевом – ближе к ν_iОПТ2.

Величину ν_iОПТ1, соответствующую максимальному значению КПД, можно получить, приравняв первую производную выражения 8.24 к нулю. Выражение ν_iОПТ1 является функцией от β и η_Т, η_К и имеет громоздкое уравнение, которое сложно анализировать. Поэтому более целесообразно проводить анализ зависимости КПД от ν при постоянных значениях величин β и η_Т, η_К графическим способом.

Величину ν_iОПТ2, соответствующую максимальному значению работы цикла, можно получить, приравняв первую производную выражения 8.23 к нулю, преобразовав его следующим образом

(8.26)

Из выражения 8.26 видно, что оптимальная степень повышения давления воздуха в компрессоре будет увеличиваться с возрастанием коэффициентов β и η_Т, η_К. При значениях η_К=1 и η_Т=1 выражение 8.26 превратиться в уравнение 8.13 для оптимального значения ν идеального цикла ГТУ. Это свидетельствует о том, что ν_iОПТ>ν_iОПТ2, т.е. в реальном цикле ГТУ оптимальное значение степени повышения давления воздуха в компрессоре меньше, чем в идеальном. При этом с увеличением Т₃ и уменьшением Т₁ (увеличением β) ν_iОПТ2 будет увеличиваться.

Аналогично ν_iОПТ2 изменяется и величина ν_iОПТ1 в зависимости от коэффициентов β и η_Т, η_К, при этом ее численное значение, оставаясь меньше ν_iОПТ2, увеличивается с увеличением β.

Графическая зависимость влияния степени повышения давления воздуха в компрессоре при двух значениях β₂>β₁ на внутреннюю работу и КПД реального цикла ГТУ показана на рис. 8.10. Из графиков видно, что увеличение β приводит к увеличению оптимальных значений ν_iОПТ1 и ν_iОПТ2, при этом происходит увеличение внутреннего абсолютного КПД ГТУ. Следовательно для ГТУ всегда целесообразно иметь максимально возможную температуру Т₃ и минимальное значение температуры Т₁.

В результате анализа экономичности действительного цикла ГТУ можно сделать вывод, что она зависит от следующих величин: ν, β, η_Т, η_К. При этом оптимальные значения ν_iОПТ1 и ν_iОПТ2 можно получить аналитическим методом, используя уравнения 8.25 и 8.26. Однако необходимо учитывать, что данные уравнения получены с целым рядом допущений (см. начало разд. 8.1). Поэтому для корректных инженерных расчетов реального цикла ГТУ необходимо учитывать зависимость изобарной теплоемкости (или энтальпии) воздуха и продуктов сгорания топлива от температуры, а также количество топлива.