
(6.20)
Такой случай смешения в технике наиболее типичен при заполнении баллона газом из магистрального газопровода с постоянным давлением (рис. 6.8).
Пусть в баллоне до смешения находится газ массой m1 и параметрами Р1, T1. При открытии вентиля из магистрали в баллон поступает другой газ массой m2 с параметрами Р2, T2. Естественно, должно выполняться условие Р2 > Р1. При закрытии вентиля устанавливаются новые параметры газа в баллоне PСМ и TСМ.
Задача состоит в определении параметров смеси при известном количестве поступившего в баллон газа m2 или при известном конечном давлении PСМ – в определении количества поступившего в него газа m2. Кроме того, необходимо оценить величину необратимости этого процесса, через увеличение энтропии системы.
Рассмотрим первую ситуацию, когда известны начальные параметры обоих газов и масса m2, поступившего в баллон газа из магистрали. После заполнения в баллоне получается смесь газов массой mСМ=m1+m2. Сразу можно определить удельный объём смеси:
 |
(6.20) |
Для определения состояния смеси газов необходимо найти второй параметр. Его можно определить из первого закона термодинамики для данной системы:
 |
(6.21) |
Будем рассматривать процесс смешения без теплообмена с окружающей средой, т.е. Q = 0. В баллон проталкивается газ массой m2, т.е. совершается внешняя работа проталкивания над газом высокого давления, равная L=Р2(0-V2)=-Р2V2. Эту работу можно трактовать как работу проталкивания в цилиндре с поршнем при подаче порции газа массой m2 с изменением объёма газа в цилиндре от V2 до 0 при постоянном давлении Р2=const.
После подстановки работы и теплоты в выражение (6.21) получим уравнение смешения при заполнении объема:
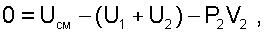 |
(6.22) |
 |
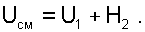 |
(6.23) |
После деления выражения (6.23) на массу смеси получаем выражение для удельной внутренней энергии смеси:
 |
(6.24) |
Используя vСМ и uСМ можно определить все остальные параметры смеси газа.
Наиболее просто определение остальных параметров выполняется для идеальных газов. Так, приняв начало отсчёта внутренней энергии и энтальпии при абсолютном нуле – 0 K, их численные значения при этой температуре будут одинаковы и равны нулю uОСМ=uО1=hО2=0, а выражение (6.24) при замене в нем внутренних энергий и энтальпий через теплоемкости и абсолютные температуры примет вид:
 |
(6.24*) |
 |
(6.25) |
Выражение 6.25 справедливо только при подстановки в него абсолютных температур, для температур в градусах Цельсия оно непригодно.
Определение давления смеси ведется по уравнению состояния идеального газа:
 |
(6.26) |
Оценка необратимости процесса смешения при заполнении объёма, через увеличение энтропии системы, рассчитывается аналогично двум предыдущим процессам смешения как:
 |
В случае если в данном процессе смешения известно давление смеси, то искомой является масса газа, поступившего в баллон m2. При решении такой задачи необходимо решать систему двух уравнений 6.25 и 6.26 с привлечением уравнения g1+g2=1, т.е. получается система трех уравнений с тремя неизвестными: g1, g2 и ТСМ. Определив массовые доли смеси газов, рассчитывается масса газа, поступившего в баллон как
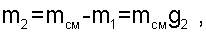 |
| предыдущий параграф | содержание | следующий параграф |