3.4.1. Аналитическое выражение первого закона термодинамики

Уравнение первого закона термодинамики (3.27) обычно записывается с расположением теплоты в левой части, а изменения внутренней энергии и работы расширения в правой

(3.29)

Для одного килограмма вещества оно примет вид:

(3.30)

Это интегральная форма записи первого закона термодинамики, т.е. целиком для всего процесса, происходящего с веществом от состояния 1 до состояния 2. Дифференциальная форма записи первого закона термодинамики, т.е. для элементарного участка процесса, будет иметь вид:

(3.31)

(3.32)

В этих уравнениях величинами L' и l' обозначается работа изменения объема, совершаемая телом в реальных необратимых процессах. Работа расширения увеличивает механическую энергию системы, т.е. она может передаваться или внешнему потребителю работы, или внешней среде. При обратимых процессах вся работа изменения объема тела затрачивается на преодоление внешнего давления и аккумулируется системой в форме механической энергии. Расчетное выражение работы изменения объема обратимого процесса было получено ранее в виде

При необратимых процессах изменения объема тела имеет место трение. Например, трение газа о стенки емкости или расширение газа идет с образованием вихревого движения. Трение приводит к увеличению внутренней энергии тела (оно нагревается). Поэтому внешняя работа расширения оказывается меньше работы изменения объема обратимого процесса на величину работы трения

(3.33)

здесь l и l'- работа обратимого и необратимого процесса,l_тр - работа трения. Работа трения l_тр переходит в конечном результате в теплоту трения dq_тр. Тогда первый закон термодинамики для необратимого процесса расширения тела можно записать в виде:

перегруппировав члены данного уравнения, окончательно получим

(3.34)

где q* - полная теплота, полученная телом в необратимом процессе. Для обратимых процессов q_тр=0, и первый закон термодинамики обратимого процесса будет иметь вид

(3.35)

Поскольку внутренняя энергия может быть представлена в виде функции любой пары независимых параметров состояния (она сама параметр состояния), то выражение (3.35) можно записать в виде частных производных от этих параметров состояния. Например, выразив du в частных производных от P и v, получим выражения

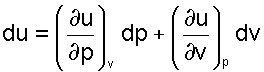(3.36)

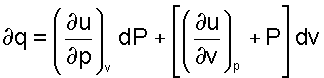(3.37)

Таких уравнений можно записать столько, сколько существует пар независимых параметров состояния. Значение дифференциалных уравнений первого закона термодинамики очень велико. Поскольку, зная функциональную взаимосвязь термических параметров состояния вещества (Р,v,T), используя эти дифференциальные уравнения, можно расчитать энергетические параметры данного вещества (u, s и т.п.) и его теплоемкости, а так же решать и обратную задачу.