3.2. Теплота, теплоемкость, энтропия

Пусть в цилиндре под поршнем (рис.3.4.) находится газовое термодинамическое тело. Закрепив поршень штифтами, исключим возможность механического взаимодействия тела с окружающей средой. Также исключим химическое, ядерное, электрическое и прочие взаимодействия тела с окружающей средой, оставив возможность только теплового энергетического взаимодействия.

В результате теплового энергетического взаимодействия, которое обусловлено наличием разных температур у нашего газа и окружающей среды, будет наблюдаться изменение температуры тела (в нашем случае увеличение), т.е. энергия газа изменилась. Мерой любого энергетического взаимодействия является работа. Назовем работу нашего примера тепловой работой или, как принято говорить, теплотой.

Теплота или тепловая работа - мера теплового энергетического взаимодействия тел, возникающая при наличии разности их температур.
Теплота имеет обозначения Q и q=Q/m – удельная теплота. Их размерности такие же, как и у работы изменеия объема [Дж] и [Дж/кг], поскольку природа их одинакова - мера энергетического взаимодейцствия. Если система состоит из нескольких тел, то ее теплота равна сумме теплот, подведенных к каждому телу. Она подчиняется закону суммирования или аддитивности, как говорят математики.

Количество передаваемой теплоты научились определять довольно точно в XYIII-XIX веках в результате развития калориметрии. Поскольку подвод или отвод теплоты связан, как правило, с изменением температуры тела, то первоначально и была получена опытным путем эта взаимосвязь в виде выражения:

(3.9)

Теплоемкость [Дж/град], исходя из (3.9), есть количество теплоты, необходимое для нагрева тела на один градус:

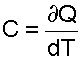(3.10)

Теплоемкость так же, как и теплота, обладает аддитивностью (свойством суммирования в зависимости от количества вещества). Отнесенная к одному килограмму массы вещества она называется удельной массовой теплоемкостью [Дж/(кг град)]:

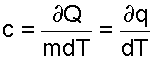(3.11)

где q - удельная теплота.

Так же как и любая другая работа, теплота есть функция процесса, о чем и свидетельствует знак неполного дифференциала "∂". Следовательно, и теплоемкость есть функция процесса. На практике широко используются удельные теплоемкости для процессов при постоянном давлении c_P - изобарная теплоемкость и постоянном обьеме c_V - изохорная теплоемкость. Необходимо отметить, что теплоемкость реальных веществ величина переменная. Она зависит от давления и от температуры вещества. Подробное изложение материала о теплоемкостях будет приведено в разделах идеальные и реальные газы.

Вернемся к теплоте. Полное ее количество с использованием теплоемкости данного процесса определяется интегрированием выражения (3.9) или (3.11)

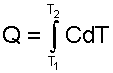(3.12)

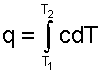(3.13)

Отметим, что разница температур в градусах Кельвина и Цельсия одинакова, то есть: 

(3.14)

                                     

Поэтому размерность теплоемкостей и расчетные формулы теплоты [Дж/кг] могут иметь обозначения изменения температуры как в градусах Кельвина, так и Цельсия

(3.15)

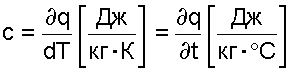(3.16)

С помощью теплоемкости не всегда возможно рассчитать теплоту. Так при фазовых переходах вещества температура тела не изменяется Т=const, но теплота фазового перехода не равна нулю q≠0. Например, при постоянном атмосферном давлении плавление льда требует подвода теплоты, при этом температура жидкой и твердой фаз воды остается неизменной и равной 0 ⁰С. В этом случае воспользоваться выражением (3.14) для определения теплоты нельзя, т.к. dt = 0, а c = ∞ .

Кроме того, природа теплоты та же, что и природа любой работы - мера энергетического взаимодействия. Следовательно, теплота может быть расчитана по формуле обобщенной работы как произведение некоторой силы F_X на изменение некоторой координаты перемещения dx в направлении действия данной силы:

(3.17)

Сила и координата перемещения должны являться функциями состояния - параметрами (аналогично Р и v для работы изменения объема ∂l=Pdv). При этом сила должна быть интенсивным параметром, а координата перемещения экстенсивным параметром состояния. Ни теплоемкость, ни изменение температуры в выражении (3.14) этим условиям не соответствуют.
В 1865 г. Клиузиусом [1] было предложено понятие энтропии S [Дж/К] (в переводе с греческого – превращение), соответствующее выражению:

(3.18)

Используя энтропию, можно получить расчетное выражение теплоты в виде:

(3.19)

Выражение (3.19) отвечает расчетному выражению теплоты, как работы. При этом абсолютная температура Т и энтропия S являются параметрами состояния: Т - интенсивный параметр, S - экстенсивный. Абсолютная температура в выражении (3.19) выступает в роли силы, а энтропия в роли координаты перемещения под действием этой силы, при совершении тепловой работы или теплоты.

Исходя из вышеизложенного дадим определение энтропии применительно к технической термодинамике.

Энтропия - параметр состояния,  соответствующий координате перемещения при действующей силе в виде абсолютной  температуры, необходимый для расчета тепловой работы (теплоты).

Принадлежность энтропии к параметрам состояния будет доказана в разделах: "Идеальные газы", "Реальные газы и пары", "Второй закон термодинамики", "Дифференциальные уравнения термодинамики". В этих разделах также будет дана и методика определения численных значений энтропии идеальных газов и реальных веществ.

В технической термодинамике понятие энтропии неразрывно связано с понятием теплоты: есть теплота, есть изменение энтропии, нет теплоты, нет изменения энтропии.

В статистической термодинамике [4] энтропия выступает в другой роли - вероятностной оценки состояния термодинамической системы. В разделе математики "теория вероятности" также пользуются понятием энтропии. Математики используют название энтропии для вероятностной оценки событий по аналогии со статистической термодинамикой, но в математике это понятие никакого отношения к теплоте не имеет.

В дальнейшем, при изучении второго закона термодинамики, понятие энтропии будет иметь более широкое значение. Необходимо отметить, что значение имеет только изменение энтропии, абсолютная величина энтропии никакой физической сути не имеет. Поскольку энтропия параметр состояния, она может быть определена любой парой независимых параметров состояния. Энтропия подчиняется закону сложения. Энтропия в расчете на килограмм вещества называется удельной энтропией [Дж/(кг К)]:

(3.20)

Изменение энтропии однозначно определяет знак теплоты. При увеличении энтропии ds > 0 теплота подводится к системе q > 0, при уменьшении энтропии ds < 0 теплота отводится q < 0.
     Используя понятие энтропии, теплоту легко графически показать в T,s- координатах (рис. 3.5). Для построения оси энтропий s в этом случае выбирают начало отсчета, соответствующее фиксированному состоянию вещества (любая пара независимых параметров состояния). Часто в качестве начала отсчета энтропии берется нормальное физическое состояние - 0 ⁰С и 760 мм рт.ст. При этих значениях принимают, что s₀ = 0, тогда разность энтропий будет иметь численное значение, равное абсолютной величине энтропии s=s-s₀, которое может быть подсчитано для данного вещества на базе выражения (3.20), путем его интегрирования от нулевого до данного состояния вещества. Причем путь интегрирования никакой роли не играет, поскольку энтропия есть параметр состояния.                                         

На рис. 3.5 в виде кривой 1-2 представлен процесс изменения состояния термодинамического тела. Заштрихованная площадка под элементарным участком процесса равняется произведению Tds и представляет элементарное количество теплоты ∂q.

Интегральная сумма таких площадок под кривой 1-2 представляет полное количество теплоты, получаемое телом в процессе 1-2:

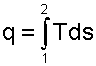(3.21)

Так как площадь под кривой процесса в T,s- диаграмме соответствует количеству теплоты, она получила называние тепловой диаграммы, аналогично Р,v- диаграмме, называемой рабочей.

В T,s- диаграмме можно графически показать теплоемкость в любой точке процесса. Например, для точки А теплоемкость будет в виде отрезка ВС, образованного касательной к точке А - АВ и проекцией точки А на ось энтропий - АС:

(3.22)

Отрезок ВС носит название подкасательной. При этом теплоемкость положительна, если подкасательная расположена слева от точки (А), и отрицательная, если справа.