9.4.1. Эксергия в объеме

В технической термодинамике наибольший интерес представляет возможность получения работы в системе, состоящей из тел и внешней среды, находящихся в неравновесном состоянии. Окружающая среда в большинстве энергетических установок выступает в качестве холодного источника теплоты: водоемы для ТЭС и АЭС, окружающий воздух для ДВС и ГТУ и т.п.. Тела, не находящиеся в равновесном состоянии с окружающей средой: продукты сгорания органического топлива, тепловыделяющие элементы ядерных реакторов и т.п., представляют собой горячие источники теплоты, т.е. они выступают в роли потенциальных источников работы. Для оценки максимальновозможного количества полезной работы, которое может быть получено в таких системах, в 1955 г. югославским ученым З. Рантом было введено понятие эксергии [5, 6].

Эксергией в объеме называется максимально возможная полезная работа постоянной массы вещества в закрытой системе, которая может быть получена при переходе данного вещества (тела) из неравновесного состояния в состояние равновесия с окружающей средой только по обратимым процессам.

Для иллюстрации понятия эксергии в объеме рассмотрим газообразное тело в цилиндре под поршнем (рис. 9.23). Тело имеет параметры P₁, T₁, окружающая среда имеет параметры P_ОС, T_ОС. Пусть эта система находится в неравновесном состоянии, т.е. P₁≠P_ОС и T₁≠T_ОС. В соответствии с определением эксергии в данной системе получается максимальная полезная работа при обратимом переходе тела из начального состояния в состояние полного термодинамического равновесия с окружающей средой.

Таким образом, эксергия в данном примере будет работой на штоке поршня при обратимом переходе тела из первоначального состояния (I с.) с параметрами Р₁, Т₁, U₁, S_.1 в состояние его термодинамического равновесия с окружающей средой (II с.), когда его давление и температура будут такими же как и у окружающей среды Р_ОС, Т_ОС,, а внутренняя энергия и энтропия тела будут определяться как функция этих параметров U_ОС=F(Р_ОС,Т_ОС), S_ОС=f(Р_ОС,Т_ОС).

Аналитическое выражение для определения эксергии получается из выражения первого закона термодинамики для тела, находящегося в закрытой системе, при совершении телом обратимых процессов.

Первый закон термодинамики для обратимого процесса имеет вид:

(9.31)

Количество теплоты, подведенное к телу в нашем примере, можно рассчитать через параметры его состояния, на основании следующих положений:

Поскольку система состоит только из нашего тела и окружающей среды, то количество теплоты, подведенное к телу, равно, взятому с обратным знаком количеству теплоты, отданному окружающей средой Q = -Q_ОС (в соответствии с первым законом термодинамики);

В системе происходят только обратимые процессы, следовательно, в соответствии со вторым законом термодинамики, изменение энтропии такой системы равно нулю ΔS_С=ΔS_Т+ΔS_ОС=0, а изменение энтропии тела равно изменению энтропии окружающей среды, взятому с обратным знаком ΔS_Т=-ΔS_ОС;

Температура окружающей среды не изменяется, следовательно, теплоту окружающей среды можно представить в виде выражения, соответствующего изотермическому процессу

(9.32)

Теплоту, полученную телом, можно рассчитать по выражению (9.30), взяв его с обратным знаком и выразив изменение энтропии окружающей среды через изменение энтропии самого тела

(9.33)

где - S₁, S_ОС - энтропия тела в начальном состоянии и в состоянии равновесия с окружающей средой (при Р_ОС и Т_ОС).

При изменении объема тело совершает работу L, но всю эту работу как полезную рассматривать нельзя. Часть работы расширения тела L расходуется на перемещение внешней среды, т.е. в нашем примере при движении поршня он перемещает внешнюю среду. Эта работа называется внешней, а так как давление внешней среды не изменяется, то она может быть подсчитана в виде выражения:

(9.34)

где V₁ и V_ОС - объем тела при начальных параметрах и при давлении и температуре окружающей среды.

Таким образом, максимальная полезная работа будет представлена в виде разности работы расширения тела и внешней работы:

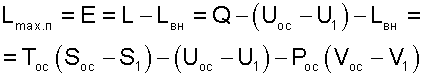(9.35)

После деления правой и левой частей выражения (9.34) на массу тела получается расчетное выражение удельной максимальнополезной работы, которое и является аналитическим выражением эксергии постоянной массы вещества в закрытой системе:

(9.36)

В выражении (9.35) параметры начального состояния тела в разностях поставлены на первое место для лучшего восприятия формулы. Из выражения (9.35) видно, что эксергия при неизменном состоянии внешней среды является функцией состояния вещества, т.е. ее можно представить в виде

(9.37)

где постоянная определяется состоянием вещества при параметрах внешней среды.

Эксергию в объеме можно представить графически в виде площади в термодинамических диаграммах Р,v и Т,s.

На рисунках 9.24 и 9.25 эксэргия идеального газа, имеющего параметры P₁, T₁, v₁, u₁, s₁, представлена в виде площади 1а2b1.

В данном примере обратимый переход идеального газа из первоначального состояния (точка 1) в состояние равновесия с окружающей средой (точка 2) осуществляется по обратимой адиабате 1а при s₁=const и обратимой изотерме а2 при Т_ОС=const.

В P,v- диаграмме площади под обратимыми процессами 1а и а2 представляют работу изменения объема данного газа. Площадь под адиабатой 1а равна изменению внутренней энергии идеального газа в интервале температур Т₁ и Т_ОС, т.е. пл.1аа'1'1=l_1а=u₁-u_ОС. Площадь под изотермой а2 равна теплоте этого процесса, т.е. пл.а22'а'а=l_а2=q_а2=T_ОС(s_ОС-s₁). Полная работа изменения объема газа на процессе 1а2 будет представлена в виде алгебраической суммы этих площадей, т.е. l_1а2= пл.1аа'1'1+пл.а22'а'а=u₁-u_ОС-T_ОС(s₁-s_ОС). При графическом суммировании этих площадей в диаграмме Р,v необходимо учитывать отрицательный знак работы на процессе сжатия газа а2 (штриховка этой площади выполнена на рис.9.24 в противоположном направлении по отношению к процессу расширения газа 1а).

Для получения эксергии необходимо из работы изменения объема газа в процессе 1а2 вычесть внешнюю работу e=l_1а2-l_ВН. Расчетное выражение внешней работы газа соответствует величине l_ВН=P_ОС(v_ОС-v₁). Внешняя работа, взятая с обратным знаком, в диаграмме Р,v соответствует площади под изобарным процессом 2в, т.е. -l_ВН=P_ОС(v₁-v_ОС)=пл.2b1'2'2 (работа процесса 2b положительная). В итоге получили, что эксэргии газа, имеющего параметры точки 1, в Р,v- диаграмме соответствует работа изменения объема процесса 1а2в. Эта работа соответствует площади

В диаграмме Т,s эксергию идеального газа, имеющего параметры точки 1, можно показать в виде площади, перенеся процесс 1а2b из Р,v диаграммы в диаграмму Т,s (рис.9.25).

Площадь под изохорой v₁=const процесса с1 соответствует изменению внутренней энергии идеального газа в интервале температур Т₁ и Т_ОС, т.е. пл.11'с'с1=u₁-u_ОС. Площадь под изотермой Т_ОС=const процесса а2 соответствует его теплоте, т.е. пл.а22'1'а=q_а2=T_ОС(s_ОС-s₁). Площадь фигуры 2bcc'2'2 соответствует работе изменения объема изобарного процесса 2b, т.е. пл.2bcc'2'2=l_2d=Р_ОС(v₁-v_ОС).

В результате алгебраического сложения площадей под процессами 1с, а2 и вычтя работу процесса 2b в диаграмме Т,s получили площадь фигуры 1a2b1, которая соответствует величине эксергии, т.е.

Показать эксергию в объеме для газа в виде площади в диаграммах Р,v и Т,s можно, используя и другие обратимые процессы перехода газа из неравновесного состояния в состояние равновесия с окружающей средой.