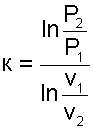
(7.30)
Для расчета процессов изменения состояния водяного пара не используются имеющиеся для него уравнения состояния, ввиду их сложности и ограничений применимости в зависимости от области параметров состояния водяного пара (в различных областях используются различные уравнения). Применение таких уравнений оправдано, когда они заложены в современные ЭВМ, и машина сама считает параметры по любой известной паре параметров по специальной программе.
Практически расчет процессов изменения состояния воды и водяного пара осуществляется с использованием таблиц их термодинамических свойств и диаграмм. Из диаграмм наибольшее применение нашли h,s- диаграммы.
Наиболее простым и наглядным является метод расчета паровых процессов с использованием h,s- диаграммы. Здесь не нужно выяснять, в какой области протекает процесс, есть ли переход из зоны перегретого пара в зону влажного пара или наоборот. Все это видно по графику процесса. Расчет сводится к чтению диаграммы и, в случае надобности, к подсчету по полученным из диаграммы данным работы, теплоты и изменений параметров и функций состояния. В случае, когда процесс выходит за пределы рабочей h,s- диаграммы, расчет проводится с использованием таблиц термодинамических свойств воды и водяного пара.
Диаграммы Р,v и T,s служат для иллюстрации особенностей процессов и могут быть применены для графического изображения в виде площадей энергетических величин q, l, Du , характеризующих данный процесс.
В практике теплоэнергетики наиболее часто встречаются: изохорный процесс (растопка котла при повышении давления), изобарный процесс (установившийся режим работы котла, процессы в подогревателях и конденсаторах пара), адиабатный процесс (в паровой турбине и насосе), изотермический процесс (испарение воды в реакторе кипящего типа).
Рассмотрим подробно эти процессы, считая их обратимыми.
В тепловых машинах, таких как турбина или насос, процесс протекает очень быстро и теплообмен с внешней средой очень незначителен, им можно пренебречь. Поэтому обратимым процессом в таких машинах является идеальная адиабата (изоэнтропа).
На рис. 7.24, 7.25, 7.26 изображен обратимый адиабатный процесс расширения пара 1-2 в Р,v-, T,s- и h,s- диаграммах.
В Р,v- диаграмме адиабата представляет собой кривую гиперболического характера с переменным показателем адиабаты "к". Необходимо отметить, что показатель адиабаты "к" для воды и пара никакого отношения к коэффициенту Пуассона cP/cV не имеет. Он рассчитывается только по параметрам обратимого адиабатного процесса вблизи какой - либо фиксированной точки по формуле
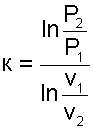 |
(7.30) |
Показателем адиабаты в расчетах процесса пользуются крайне редко ввиду того, что он - величина переменная. Его численные значения сильно отличаются друг от друга в различных точках адиабатного процесса: чем дальше расположены точки, тем больше разница. При переходе процесса из области перегретого пара в область влажного насыщенного эта разница еще больше увеличивается.
Площадь под процессом 1-2 в Р,v- диаграмме есть работа расширения, а поскольку
то работа расширения адиабатного процесса равна изменению внутренней энергии с обратным знаком и может быть подсчитана как
(7.31) |
В формуле (7.31) при расчетах следует обратить внимание на соответствие размерностей энтальпий и произведений Pv.
В Т,s- и h,s- диаграммах обратимый адиабатный процесс представляет вертикальную прямую (s=const - изоэнтропа). Представление энергетических характеристик (lS, Du) в Т,s- и h,s- диаграммах возможно с помощью дополнительных построений, но это не имеет практической ценности. В h,s- диаграмме разность энтальпий адиабатного процесса представляет работу изменения давления в потоке l0 = h1 - h2 (техническая работа в турбине, насосе и т.п.). С понятием этой работы познакомимся позднее при изучении процессов теплоэнергетических установок.
Изохорный процесс может иметь место в случае теплообмена с внешней средой водяного пара, находящегося в сосуде постоянного объема. На рис. 7.27, 7.28, 7.29 изображен изохорный процесс 1-2 в Р,v-, T,s-, h,s- диаграммах.
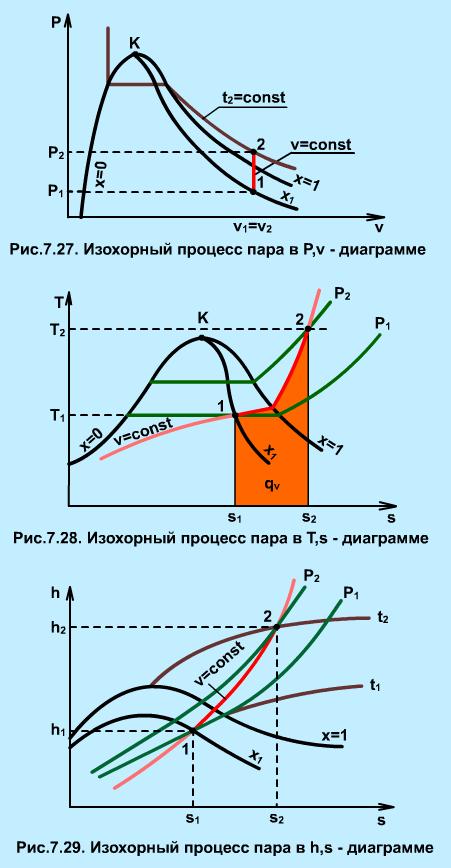 |
В Р,v- диаграмме изохора 1-2 - вертикальная прямая (рис.7.27). Работа расширения в изохорном процессе равна нулю (dl=Рdv, dv=0, lV= 0). Теплота изохорного процесса расходуется только на увеличение внутренней энергии пара:
(7.32) |
В диаграмме Т,s теплота qV изображается площадью под изохорным процессом 1-2 (рис. 7.28). Эта же площадь соответствует изменению внутренней энергии изохорного процесса. Поскольку s2 > s1, теплота и изменение внутренней энергии процесса 1-2 положительные.
По диаграмме h,s можно определить все необходимые параметры состояния (рис. 7.29) для расчета теплоты и изменения внутренней энергии изохорного процесса.
На рис. 7.30, 7.31, 7.32 изображен изобарный процесс 1-2 в Р,v-, T,s-, h,s- диаграммах. Точка 1 этого процесса находится в области влажного насыщенного пара, поэтому может быть задана любой парой параметров состояния, кроме Р1 и t1, так как в этой области изобара совпадает с изотермой. Вторая точка находится в области перегретого пара и задается любой парой параметров.
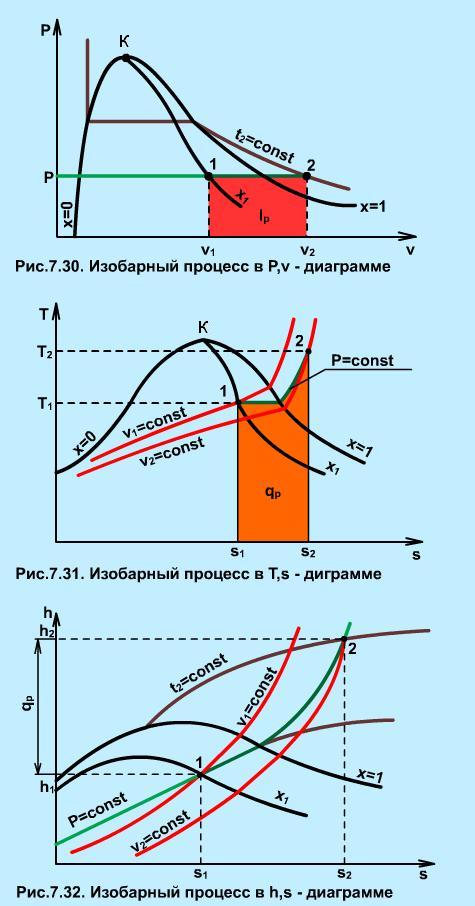 |
В диаграмме Р,v изобара представляет горизонтальную прямую 1-2 (рис. 7.30), площадь под которой соответствует работе расширения, определяемой по формуле
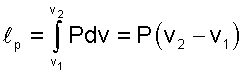 |
(7.33) |
Количество теплоты в изобарном процессе соответствует изменению энтальпии (q = dh - vdР, dР = 0, dqP = dhP) и определяется как
(7.34) |
В Т,s- диаграмме (рис. 7.31) теплота qP представлена площадью под процессом, в h,s- диаграмме (рис. 7.32) - отрезком прямой в виде разности ординат. Изменение внутренней энергии изобарного процесса подсчитывается по формуле
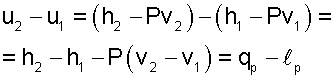 |
(7.35) |
На рис. 7.33, 7.34, 7.35 изображен изотермический процесс 1-2 в Р,v-, T,s-, h,s- координатах. Определение параметров в начальной и конечной точках процесса аналогично предыдущим процессам.
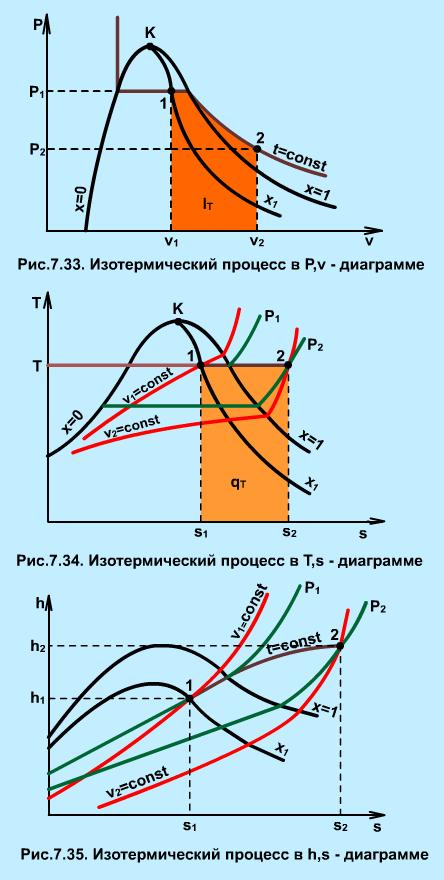 |
Работа расширения изотермического процесса изображается площадью под процессом 1-2 в Р,v- координатах (рис. 7.33) и рассчитывается исходя из первого закона термодинамики:
(7.36) |
В Т,s- диаграмме изотерма - горизонтальная прямая. Площадь под изотермическим процессом 1-2 в T,s- диаграмме представляет теплоту (рис. 7.34), которая может быть подсчитана по формуле
(7.37) |
В h,s- диаграмме (рис. 7.35) изотерма 1-2 - сложная кривая линия в области влажного пара, совпадающая с изобарой. Подсчет изменения внутренней энергии изотермического процесса ведется традиционным для водяного пара образом, через энтальпию:
| предыдущий параграф | содержание | следующий параграф |